Featured image of post 阅读笔记：LoRA without Regret
搞搞技术

阅读笔记：LoRA without Regret

Thinking Machines的博客，我愿翻译为“我LoRA无悔”（大雾）

TL;DR

本文是对LoRA Without Regret的阅读笔记。这篇博客主要想讨论的内容是LoRA和全参数微调（FullFT）的性能对比。核心观点是：在特定条件下，LoRA可以达到全参微调（FullFT）完全相同的性能和样本效率。

这样的特定条件包括两个关键：

  1. 将LoRA应用于所有层，而不是只有Attention
  2. LoRA rank不能小到无法容纳数据集的信息量

Prerequisite

（基于回忆，可能不够严谨）

LoRA：low rank adaptor

由于Transformer中的参数是高度稀疏的（无论是Attention的四个矩阵还是FFN），而其参数更新也是；所以我们可以用两个低秩矩阵的乘积代替一个高秩矩阵，参数更新矩阵是：

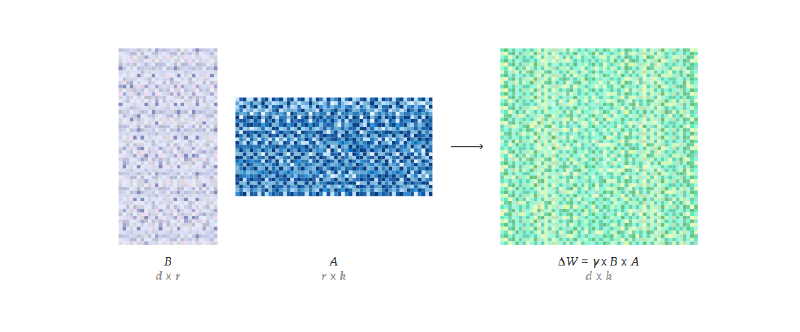
$$\Delta W \in \R^{d\times k} = B\times A,\qquad \text{where}\ B\in\R^{d\times r}\ and\ A\in\R^{r\times k} \quad r\ll\min(d,k)$$

也就是说原本的

$$h=W_0x\quad \Rightarrow \quad h'=W'x=(W_0+\Delta W)x=W_0x+BAx$$

其中一般用于降维的矩阵A会被正态初始化；用于升维的B会被0初始化（没啥差别，只是LoRA作者发现这样性能比较好）。

而虽然理论上这种低秩Adaptor的思路可以应用于所有矩阵上，但实际上长久以来只是被用于Attention的四个矩阵（Q、K、V、O），尤其是Q和V矩阵。主要是考虑实现简单和参数高效。

Main Content

这里作者使用的LoRA中多了一个缩放因子$\gamma$，也就是 $\gamma BA$，这不重要，上面就不改了。

这篇博客主要想讨论的内容是LoRA和全参数微调（FullFT）的性能对比。问题在于：LoRA能否匹敌全参微调的性能？如果能、条件是什么？

What matters for LoRA

作者们提前声明了实验设置，与以往的LoRA实验有些不同：

  1. 研究了训练集大小和LoRA参数量的关系，而不是在某个特定的数据集、任务上做实验；
  2. 用了对数loss来衡量性能，而不是跑下游评估。

最终结论是：

  1. 在中小型指令微调/推理的数据集上，LoRA和FullFT表现一样。
  2. 对于超出了LoRA容量的数据集，LoRA表现不如FullFT。但LoRA不会有一个明显的loss下界，而是训练效率更低。
  3. 在某些场景下，LoRA对较大batch size的容忍度更差——当batch size超过某些点时，loss表现更差；这种代价不会随着增加LoRA rank而变化；这是由于矩阵乘法引入的，和原本优化最初权重矩阵不一样。
  4. 即使在少量数据上，LoRA用于所有权重矩阵的效果都更好；尤其是MLP和MoE层。仅仅应用于Attention层的LoRA（为了保持训练参数一致，其rank很高）效果更差。
  5. 在强化学习上，用小rank的LoRA也和FullFT表现一样。强化学习上需要的“容量”很小，这也符合基于信息论的预期

也探讨了超参数的影响（主要是学习率），init scale和multiplier事不变量，而由于1/r的因子，学习率与rank几乎是独立的。在数据集大小和LoRA参数的影响下，LoRA和FullFT表现相近。

Methods and results

作者的实验设置：

  1. LoRA rank从1到512（10档，$2^n$），与FullFT对比。
  2. 为了消除潜在的（次优的）学习率的混杂因素，在每一个实验条件下都变化了学习率（然后所有学习率中取最优结果，也就是最低loss）。使用了常数学习率调度（也就是没有warmup或者cooldown，学习率自始而终都是常数）
  3. 用了Llama3和Qwen3系列模型，包括MoE
  4. 主要的有监督训练的数据集用了Tulu3和OpenThoughts，前者是指令微调，后者是推理。
  5. 强化学习实验用了数学推理任务，答案准确性作为reward。

对于LoRA rank： 下面是单个epoch的训练结果，每一个点都取当前训练步骤下所有学习率中最低的loss结果。（纵轴是负对数损失NLL）

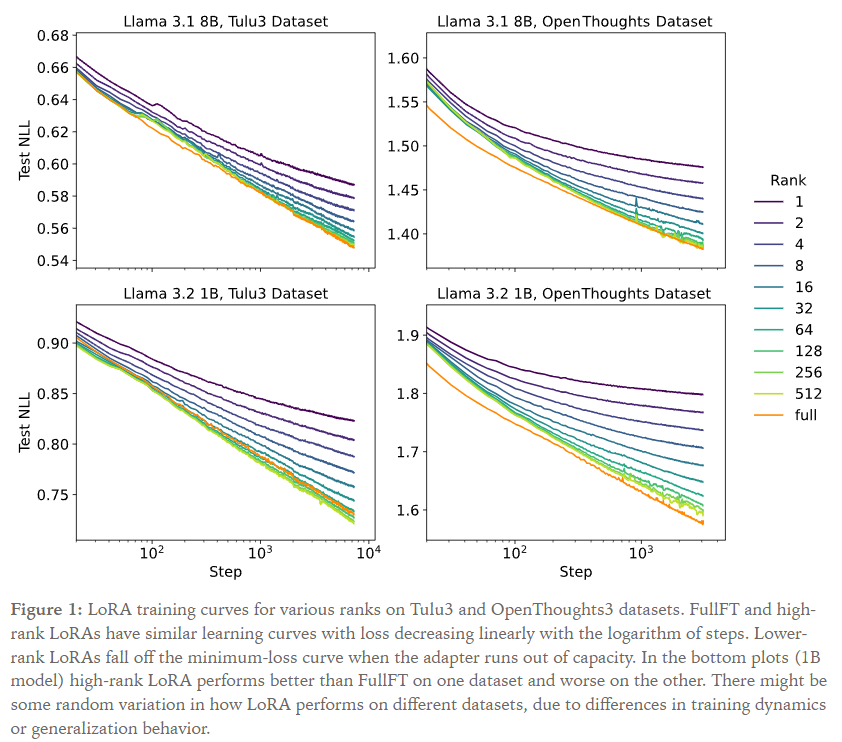
figure 1

能看得到，FullFT和high-rank LoRA的曲线接近（标记一下，最高的rank 512也只是llama3-1B的hidden size的四分之一），在最低的地方high-rank LoRA在一个数据集上比FullFT好、在其他数据集上更差。中低rank的LoRA在某些步骤（阈值与rank相关）之后偏离了最低loss曲线。直觉上来说，rank影响可训练参数量，即容量，如果容量满了，训练就会慢下来。

接下来讨论对于每个rank选择来说最优的学习率

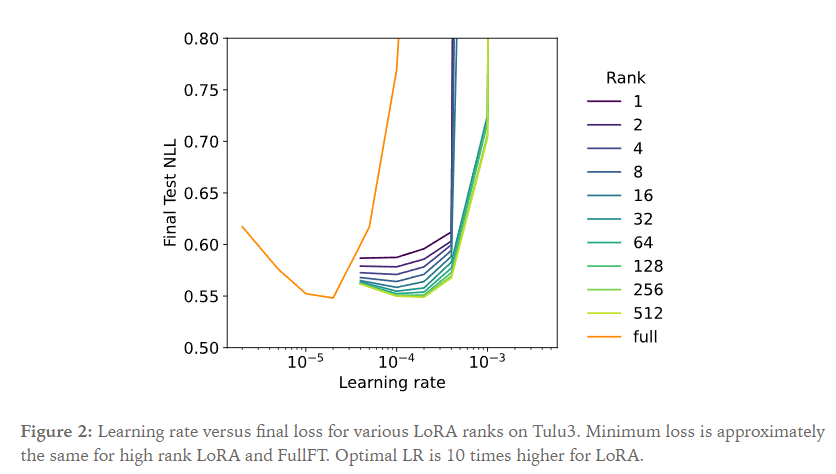
figure 2

能看得到，high-rank的最优学习率差不多是FullFT的十倍。而这个最优学习率看上去不受不同rank的影响，rank=4和rank=512的最优学习率差了不到两倍。

接下来是batch size的影响

对于较大的batch size，性能差距和rank相对是独立的。

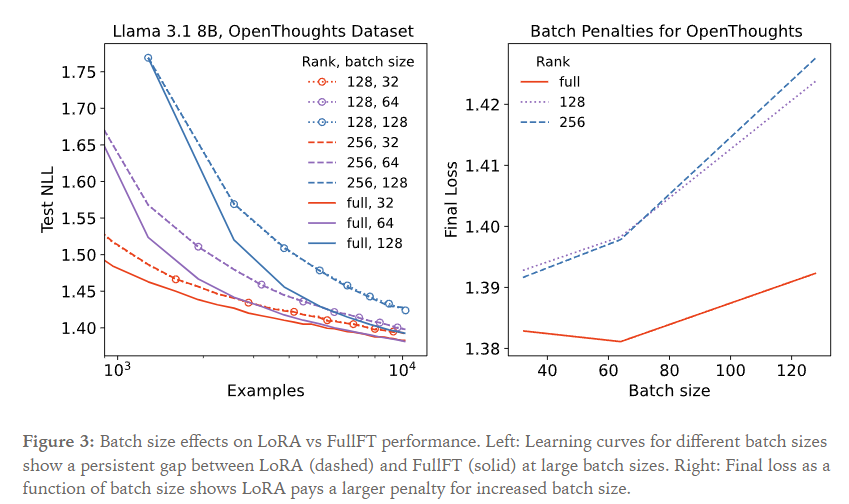
figure 3

（为啥rank=128和rank=256两条曲线的NLL几乎重合了，这和figure1不太一样啊）

能看得到：左图表现了LoRA和FullFT在大batch size下始终存在的差距；而对于小的batch size（32）这个差距随着训练变小了。右图将最终loss作为batch size的函数画了出来。

看上去在大batch size下的差距不取决于rank，一个可能的原因是矩阵乘积BA的优化动力不如全参数矩阵W，而在小batch size下二者都能实现最优loss，因而这个差距影响不大。 （我觉得很扯淡，lora rank从512缓慢变化到2048，LoRA也就退化成了FullFT，如果这个gap是与rank无关的，那这个gap会出现在哪里以及在哪里消失？）

Layers where LoRA is applied

调查了将LoRA用于不同层的效果。原始LoRA论文推荐只将LoRA用于attention矩阵，许多后续的文章也这么做了，近期趋势是应用于所有层。

作者认为应用于所有层效果更好（尤其是MLP层），只应用于attention矩阵不比只用于MLP效果好。

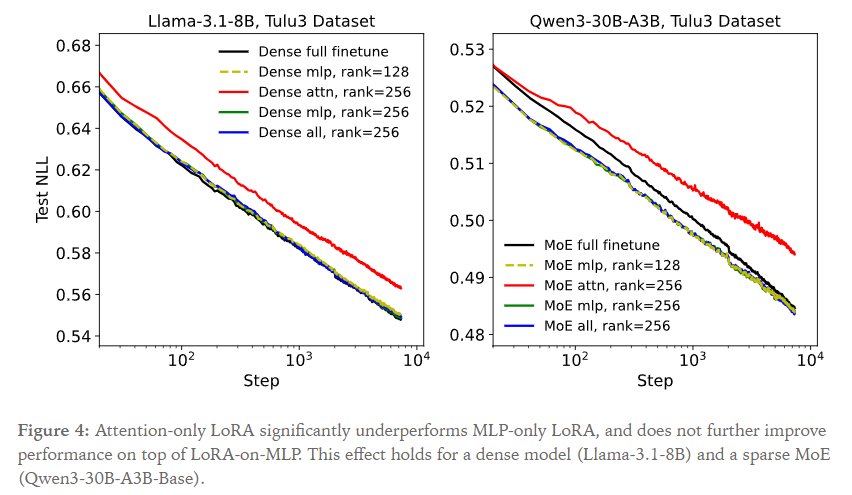
figure 4

而这和参数量更少无关，比如说，rank为256的attention-only不如rank为128的MLP-only，尽管二者的可训练参数是差不多的。

LoRA configuration Params
mlp, rank=256 0.49B
attn, rank=256 0.25B
all, rank=256 0.70B
mlp, rank=128 0.24B

（我认为直觉上来说，问题出在 $d\times 256\times 2$ 的容量大于 $d\times 128\times 4$，尽管可训练参数一样，可能由于固定损失/噪声等等，多个矩阵带来负面影响。但难以解释MoE的FullFT甚至不如LoRA）

对于MoE的实验，在每个专家上训了彼此分离的LoRA，总的rank由激活专家均分。这样也保证了参数量一致。

和上面的实验设置类似，额外增加了：

  1. rank=256在OpenThoughts3的小子集上有监督训练
  2. 在MATH上做强化学习 而在这样的设置下，MLP $\approx$ MLP+attention > attn-only也是成立的。

而对于强化学习，一个主要的实验发现是即使rank低到1，LoRA和FullFT的性能接近。

强化学习的 $\text{objective} = \sum_t\frac{p_{learner}}{p_{sampler}}Adv_t$，做法类似GRPO（每个问题采样多个输出，求组间的reward均值）。LoRA展示了性能不错的学习率的范围；以及在一定精度内和FullFT一样的性能峰值。而从图上来看，Final Reward 与 Learning Rate 的曲线和LoRA rank是相对无关的（从1到256的曲线接近，但与FullFT有一些差异）。观察到，当为每种设置选择最佳学习率时，不同大小的LoRA和FullFT的训练进展几乎完全相同。

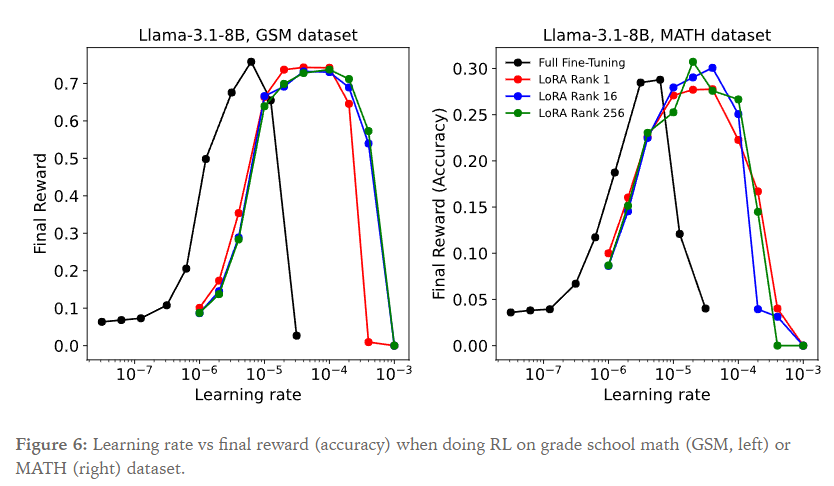
figure 6

对此的信息论解释是：监督学习提供了每个sample O(number of tokens)个bit的信息，而对于策略梯度方法，advantage只能提供 O(1) 个bit。当每个sample包含了上千个token的时候，强化学习吸收的信息就比监督学习少了上千倍。

对比着实验来说，MATH数据集中，每个问题采样32个sample，~10000个问题。假设每次completion提供了1 bit信息，整个训练吸收了320k bits，而Rank-1的LoRA（对于Llama-3.1-8B）也有着3M参数。所以LoRA的容量足以吸收所有信息，都是高度未充分训练的就体现不出什么区别。

作为对比而言，DeepSeek-R1-Zero在5.3M个sample上训练，也就是5.3M bits。这个数量少于low rank LoRA，因而作者预测这个结果可以用LoRA复现。

Setting LoRA hyperparameters

最佳学习率和rank：采用前人的做法，考虑：$W’=W+\frac{\alpha}{r}BA,\quad取\alpha=32$。

而1/r的缩放因子使得最优学习率几乎独立于rank，事实上，更强的结论成立：训练开始时学习曲线都完全相同，与rank无关。而在较长的训练周期中，学习率才会与rank相关。

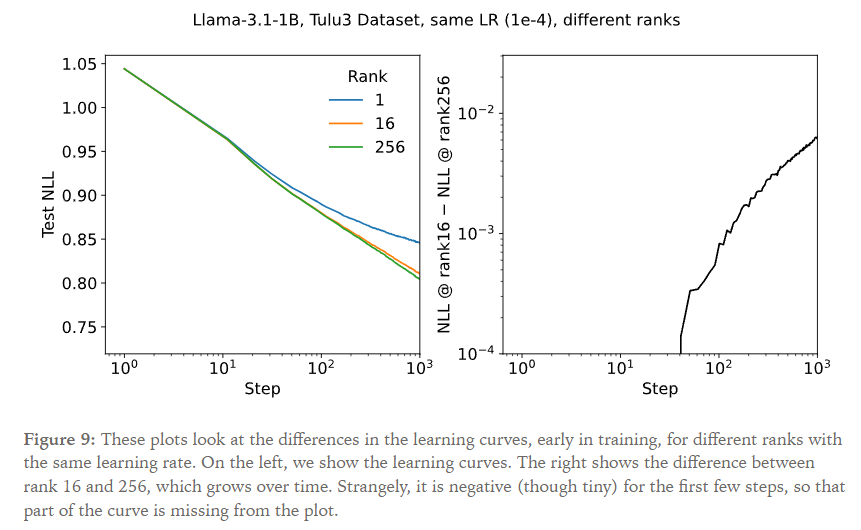
figure 9

可以通过观察第一次训练更新后LoRA矩阵的期望更新来部分地解释这个现象：将BA视作r个rank为1的外积之和：$BA = \sum_{i=1}^rb_ia_i^T=\sum_{i=1}^r\Delta_i$

于是，$\frac{\partial{\text{Loss}}}{\partial{\Delta_i}}$对于所有i都是一样的；然而梯度 $\partial{\text{Loss}}/\partial{b_i}$ 和 $\partial{\text{Loss}}/\partial{a_i}$ 将取决于A、B矩阵的初始值。（当然我前面提到一般情况下出于性能考虑，A会被正态初始化；B会被0初始化。这样的话对a的偏导项为0）。由于两个矩阵的初始化不依赖于rank，所以 $E[\Delta_i]$ 对所有i都一样，在第一步，每一步的期望更新都相同。因而也就不依赖于rank。

超参数中的不变量

一共有四个超参：

  1. 缩放因子$\alpha$
  2. 下投影矩阵A的学习率 $LR_A$
  3. 上投影矩阵B的学习率 $LR_B$
  4. 初始化 $\text{init}_A$（对于随机初始化，A是标准差，B是0，也就没必要定义 $\text{init}_B$）

实际上由于不变量的约束，四个超参里有两个是冗余的。这个不变量的约束数量通过以下双参数变换引入（优化过程是不变的）：

For p, q > 0:

  • $\alpha\rightarrow\frac1{pq}\cdot\alpha$
  • $\text{init}_A\rightarrow p\cdot\text{init}_A$
  • $LR_A\rightarrow p\cdot LR_A$
  • $LR_B\rightarrow q\cdot LR_B$

所以可以选择下面这组易于解释的基：${\alpha\cdot\text{init}_A\cdot LR_B}\quad\times\quad{\text{init}_A/LR_A}$。其中第一个基决定了初始更新的大小，也就是学习曲线的初始斜率；第二个基是一个时间尺度，也就是需要多少步能让A（从初始状态）产生显著的变化。

在这个基上，我们可以重新解释一些关于LoRA的提议，过多的不抄了，这里涉及到一篇unsloth的LoRA超参指南。

原文没有过多提及，作为补充，我对这篇unsloth的指南做一些摘要。

  • rank取8、16、32、64、128，unsloth默认16，高rank会增加模型容量，但也会增加内存使用；
  • alpha取16或者32，unsloth默认16；
  • Dropout取0~0.1，这是防止过拟合的，没什么用，默认0；
  • Weight Decay取0.01~0.1，这是一个惩罚项，防止部分权重太大，这一项不要设置太大！；
  • Warmup Steps取总步数的5%~10%，这是训练开始时逐渐提高学习率的选项；
  • Scheduler Type取线性或者余弦，这是用来在训练期间动态调整学习率的；
  • seed也就是random state，固定就行；
  • target modules：用在哪些矩阵。注意力层包括：q_proj, k_proj, v_proj, o_proj；MLP层包括：gate_proj, up_proj, down_proj；默认会作用于这7个矩阵；
  • 有效batch size：也就是batch size乘gradient accumulation steps，一般来说大点会更稳定、更平滑，一个参考值是取16左右；

在作者们的实验中，采取了标准的参数：A使用 $1/\sqrt{d_{in}}$ 的标准分布，B使用零初始化，二者使用同一个学习率，$\alpha=32$。

LoRA和FullFT的最优学习率

简而言之：LoRA的最优学习率应当始终是FullFT的10倍（也就是与预训练差不多的LR）

目前还没有充分的理论解释，因为从“最佳LoRA的LR和rank无关”、“full-rank LoRA和FullFT效果差不多”来说，LR的比率应该是模型的hidden size除以 $2\alpha$（对于1B模型也就是32左右，8B模型大概会在64）。这和实验结果不一致。

实验结果的拟合函数是：

$$\text{LR}=M_{\text{LoRA}}\cdot\left(\frac{2000}{\text{hidden size}}\right)^{\text{model pow + LoRA pow}}$$

其中：

  • $M_{\text{LoRA}}$ 是一个对于LoRA生效的乘数（FullFT为1）
  • $\text{model pow}$ 是一个指数调整项，对于Llama、Qwen等需要单独计算
  • $\text{LoRA pow}$ 是一个LoRA的调整项
  • hidden size是模型残差连接的维度

最终线性插值拟合出来的 $M_{\text{LoRA}}=9.8$，且 $\text{LoRA pow}=0$

短期和长期训练的学习率

训练刚开始的时候，由于B初始化为0，所以A的变化对BA也没啥影响。随着B变大，有效学习率增加。最终发现B矩阵的谱范数（spectral norm）会比A更大。

这意味着对于短期训练，学习率要高一点（比如FullFT的15倍）；对于长期训练，收敛到10倍左右。

Discussion

对于两个主要结论：

  1. LoRA被应用于所有层
  2. 只要容量不限制，LoRA表现很良好

LoRA在达到容量上限之前，和FullFT的学习曲线很相似。

为啥要应用于所有层

对此的一个可能的解释是关于将empirical neural tangent kernel (eNTK)看作小量微调的近似。

下面这些我没读过eNTK，看不懂，简而言之的思路是参数最多的层对kernel的影响最大。而只有将LoRA应用于包含点积的层时，eNTK(LoRA) $\approx$ eNTK(FullFT)，所以此时LoRA训练近似于FullFT。

监督学习和强化学习需要多少容量

那就算呗，一个参数存储2bit信息（这个结果依赖于精心构建的包含精确信息量的合成数据集）听上去很有意思这篇文章加入to read list。而一些经典的实验表示：最小化对数损失的时候，第一轮训练总的对数损失就衡量了数据集的description length。这个数的上街就是记忆整个数据集需要的bit数的上界。对于LLM数据集，通常每个token的loss约为1bit。

这是一个理想的记忆数据集需要的容量，高估了实际容量。如何衡量监督学习的容量需求，以及容量和可训练参数的关系，依然是留给未来工作的一个问题。

对于RL，我们认为策略梯度算法大概每个sample（episode）学习1bit的信息（是因为一个episode只得到一个reward）。

可以用信息论论证一下这个论点，将一个episode（trajectory和reward）视作一个噪声信道，这个噪声信道能提供一些关于未知奖励函数R的信息。那么policy gradient estimator和R之间的互信息，强化学习的每轮更新会是 $G=S\cdot Adv, \quad S=\nabla\log p_\theta(\tau)$，其中S与R无关，所以和R相关的部分是标量Advantage。

那么根据数据处理不等式：

$I(G; R | \text{history}) \le I((S, \text{Adv}); R | \text{history}) = I(\text{Adv}; R | S, \text{history}) \le H(\text{Adv}).$

如果将Advantage量化为B个bins，那么 $H(\text{Adv}) \lesssim \log(B)$。也就是说，每个episode学习到的有用信息是O(1) bit。当然这是一个上界。

LoRA中计算高效的Advantage

考虑一下计算效率，最终结论是LoRA每轮的FLOPS会略多于FullFT的2/3。

首先考虑FullFT的计算量：

  1. 前向 $N^2$ 次运算（乘加）：$y = Wx$
  2. 后向 $2\times N^2$ 次运算：$\bar{x} = W^T \bar{y}\quad\bar{W} += x \bar{y}^T$

而LoRA由于 $\bar{W}$ 的更新开销非常小，所以后向第二步只需要 $6NR$ 次运算，前向和后向的第一步不变，总的计算量是：$2N^2+6NR$，这就比 $3N^2$ 的2/3略多一点

Open questions

  • Sharpening our predictions of LoRA performance and the precise conditions under which it matches full fine-tuning. We have roughly characterized the regime of equal performance and can estimate the required capacity in terms of tokens or episodes, but we can’t yet make accurate forecasts.
  • Our theoretical understanding of LoRA learning rates and training dynamics is limited. A fuller theory that explains the ratio between LoRA and FullFT learning rates would be valuable.
  • How do LoRA variants such as PiSSA perform when measured according to the methodology in this article?
  • There are various options for applying LoRA to MoE layers. LoRA users would benefit from an investigation into how well they perform, and how compatible each approach is with methods like tensor parallelism and expert parallelism that are important for large MoE models.

Main Citations

Schulman, John and Thinking Machines Lab, “LoRA Without Regret”, Thinking Machines Lab: Connectionism, Sep 2025.

Unsloth, “LoRA Hyperparameters Guide”, Unsloth Documentation: Get Started, Sep 2025.